Inleiding
Beschouw de n ◊ n matrix A.
| A
= |
 |
a11 |
a12 |
. |
. |
. |
a1n |
 |
| a21 |
a22 |
. |
. |
. |
a2n |
| . |
. |
|
|
|
. |
| . |
. |
|
|
|
. |
| . |
. |
|
|
|
. |
| an1 |
an2 |
. |
. |
. |
ann |
Wij gaan ons nu
bezig houden met een functie van de n ◊ n
matrix A. Zo'n functie van de matrix A zullen we de determinant
van de matrix A noemen. Bij het ontwikkelen van de
matrixrekening hebben wiskundigen een aantal eigenschappen
geformuleerd waaraan de determinantfunctie moet voldoen om
bruikbaar te zijn bij allerlei praktische rekenproblemen.
Een van de eisen
is dat de eigenschappen van de determinantfunctie naadloos moeten
aansluiten bij de Gauss-Jordan eliminatiemethode. Bij de
Gauss-Jordan methode spelen een drietal elementaire rij-operaties
bij matrices een belangrijke rol:
-
twee rijen
verwisselen
-
een rij met
een scalair  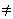 0 vermenigvuldigen;
0 vermenigvuldigen;
-
bij een rij
een  -voud
van een andere kolom optellen. -voud
van een andere kolom optellen.
Deze operaties
spelen een hoofdrol bij het bepalen van de inverse matrix A-1
en bij het oplossen van grote stelsels vergelijkingen. Alleen als
de waarde van de determinant van een matrix A 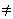 0 is, bestaat de inverse matrix A-1.
Stelsels van n lineaire vergelijkingen met n
onbekenden hebben precies ťťn oplossing als de determinant van
de coŽfficiŽntenmatrix
0 is, bestaat de inverse matrix A-1.
Stelsels van n lineaire vergelijkingen met n
onbekenden hebben precies ťťn oplossing als de determinant van
de coŽfficiŽntenmatrix 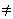 0 is. De naam 'determinant' is dus niet zonder reden gekozen.
0 is. De naam 'determinant' is dus niet zonder reden gekozen.
Tegenwoordig
gebeurt het berekenen van de determinant m.b.v.
computerprogramma's. Het algoritme hiervoor is dankzij de
rij-eigenschappen van de determinantfunctie makkelijk te begrijpen
en eenvoudig te programmeren. Hierbij speelt de Gauss-Jordan
methode een belangrijke rol. In het online matrixprogramma dat u
op deze website aantreft wordt van elke ingevoerde of berekende
vierkante matrix de waarde van de determinant direct op het scherm
afgedrukt.
Bij de
behandeling van rangschikkingen
is de determinantfunctie van een vierkante n ◊ n
matrix A reeds gedefinieerd. Voor een goed begrip van de
definitie van de determinant is het beslist noodzakelijk de
onderwerpen permutaties
en rangschikkingen
eerst te bestuderen.

Definitie
van de Determinant
Beschouw de n ◊ n matrix A.
| A
= |
 |
a11 |
a12 |
. |
. |
. |
a1n |
 |
| a21 |
a22 |
. |
. |
. |
a2n |
| . |
. |
|
|
|
. |
| ar1 |
ar2 |
. |
. |
. |
arn |
| . |
. |
|
|
|
. |
| an1 |
an2 |
. |
. |
. |
ann |
Stel V = { i
| i = 1,2, ..., n!} is de verzameling van
alle n! - zowel even als oneven - permutaties i
| i = 1,2, ..., n!} is de verzameling van
alle n! - zowel even als oneven - permutaties  i
van de natuurlijke getallen 1, 2, ... , n
met n i
van de natuurlijke getallen 1, 2, ... , n
met n  2. Door de permutatie
2. Door de permutatie  i
gaat de rangschikking i
gaat de rangschikking
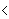 1,
2, ... , n 1,
2, ... , n dus over in de rangschikking
dus over in de rangschikking 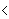  i(1), i(1),
 i(2),
... , i(2),
... ,  i(n) i(n) . Om
de leesbaarheid van de definitie wat te verhogen noteren we in de
hierna volgende definitie het matrixelement aij
als a[i, j]. . Om
de leesbaarheid van de definitie wat te verhogen noteren we in de
hierna volgende definitie het matrixelement aij
als a[i, j].
Voorbeeld
1
Beschouw de 2 ◊ 2 matrix A
| A
= |
 |
a11 |
a12 |
 |
| a21 |
a22 |
De 2 mogelijke
rangschikkingen van de kolom-indices 1 en 2 zijn:
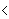 1,
2 1,
2 waarbij
waarbij  1(1)
= 1, 1(1)
= 1,  1(2)
= 2 en sgn( 1(2)
= 2 en sgn( 1)
= +1 want 1)
= +1 want  1
is even 1
is even
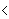 2,
1 2,
1 waarbij
waarbij  2(1)
= 2, 2(1)
= 2,  2(2)
= 1 en sgn( 2(2)
= 1 en sgn( 2)
= -1 want 2)
= -1 want  2
is oneven 2
is oneven
Hierin stellen  i
voor i = 1 en 2 de 2 mogelijke permutaties van {1, 2}voor. i
voor i = 1 en 2 de 2 mogelijke permutaties van {1, 2}voor.
|
Daaruit volgt det A = |
a11 a22
- a12 a21
|
Voorbeeld
2
Beschouw de 3 ◊ 3 matrix A
| A
= |
 |
a11 |
a12 |
a13 |
 |
| a21 |
a22 |
a23 |
| a31 |
a32 |
a33 |
De 6 mogelijke
rangschikkingen van de kolom-indices 1, 2 en 3 zijn:
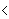 1,
2, 3 1,
2, 3 waarbij
waarbij  1(1)
= 1, 1(1)
= 1,  1(2)
= 2, 1(2)
= 2,  1(3)
= 3 en sgn( 1(3)
= 3 en sgn( 1)
= +1 want 1)
= +1 want  1
is even 1
is even
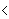 1,
3, 2 1,
3, 2 waarbij
waarbij  2(1)
= 1, 2(1)
= 1,  2(2)
= 3, 2(2)
= 3,  2(3)
= 2 en sgn( 2(3)
= 2 en sgn( 2)
= -1 want 2)
= -1 want  2
is oneven 2
is oneven
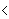 2,
1, 3 2,
1, 3 waarbij
waarbij  3(1)
= 2, 3(1)
= 2,  3(2)
= 1, 3(2)
= 1,  3(3)
= 3 en sgn( 3(3)
= 3 en sgn( 3)
= -1 want 3)
= -1 want  3
is oneven 3
is oneven
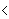 2,
3, 1 2,
3, 1 waarbij
waarbij  4(1)
= 2, 4(1)
= 2,  4(2)
= 3, 4(2)
= 3,  4(3)
= 1 en sgn( 4(3)
= 1 en sgn( 4)
= +1 want 4)
= +1 want  4
is even 4
is even
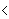 3,
1, 2 3,
1, 2 waarbij
waarbij  5(1)
= 3, 5(1)
= 3,  5(2)
= 1, 5(2)
= 1,  5(3)
= 2 en sgn( 5(3)
= 2 en sgn( 5)
= +1 want 5)
= +1 want  5
is even 5
is even
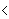 3,
2, 1 3,
2, 1 waarbij
waarbij  6(1)
= 3, 6(1)
= 3,  6(2)
= 2, 6(2)
= 2,  6(3)
= 1 en sgn( 6(3)
= 1 en sgn( 6)
= -1 want 6)
= -1 want  6
is oneven 6
is oneven
Hierin stellen  i
voor i = 1,2, ..., 6 de 6 mogelijke permutaties van {1, 2,
3}voor. i
voor i = 1,2, ..., 6 de 6 mogelijke permutaties van {1, 2,
3}voor.
|
Daaruit volgt det A = |
a11 a22
a33 -
a11 a23 a32
- a12 a21
a33 + a12 a23
a31 + a13 a21
a32
|
| |
-
a13 a22 a31
|

Elementaire
rij-eigenschappen
De determinant van A is een functie van de
matrixelementen aij en wordt vaak genoteerd als
| det
A = |
 |
a11 |
a12 |
. |
a1k |
. |
a1n |
 |
| a21 |
a22 |
. |
a2k |
. |
a2n |
| . |
. |
|
|
|
. |
| ar1 |
ar2 |
|
ark |
|
arn |
| . |
. |
|
|
|
. |
| an1 |
an2 |
. |
ank |
. |
ann |
Om de
rij-eigenschappen van de determinant op een overzichtelijke manier
te formuleren voeren we eerst een wat handiger notatie voor de
determinantfunctie in. We noteren de rijen van matrix A als
rijvectoren A1, A2, ... , An.
De re rij van A komt dus overeen met een
rij-vector van de vorm:
Ar
= (ar1, ar2,
... , arn)
We
beschouwen nu de determinant als een functie van de n
rijvectoren A1, A2, ..., An
en schrijven dit als:
det A
= d(A1, A2, ... , Ar,
... , An)
M.b.v.
deze notatie kunnen we de elementaire rij-eigenschappen op een
overzichtelijke manier formuleren. De definitie van de
determinantfunctie is zo gekozen dat deze functie de volgende
elementaire rij-eigenschappen heeft:
| |
-
Worden
de elementen van een rij Ar van de
matrix A = (aij)
met een constante  vermenigvuldigt, dan geldt:
vermenigvuldigt, dan geldt:
d(A1,
A2, ... , ∑ Ar, ... , An)
=
∑ Ar, ... , An)
=  ∑ d(A1, A2,
... , Ar, ... , An)
∑ d(A1, A2,
... , Ar, ... , An)
Det A
gaat dus over in  ∑ det A. Hierbij is dus
∑ det A. Hierbij is dus  ∑ Ar= (
∑ Ar= ( ar1, ar1,
 ar2,..., ar2,...,
 arn) arn)
-
Voor
elke r geldt:
d(A1,
A2, ..., Ar + C,
..., An) = d(A1,
A2, ..., Ar, ..., An)
+ d(A1, A2,
..., C, ..., An)
met Ar
+ C = (ar1 + c1,
ar2 + c2,
..., arn + cn) en C
= (c1, c2, ...,cn).
-
Verwisselt men in
matrix A = (aij)
twee rijen, dan wisselt det A alleen van
teken.
d(A1,
A2, ..., Ar, ..., Al,
..., An) = -
d(A1, A2,
..., Al, ..., Ar,
..., An)
-
De
determinant van de eenheidsmatrix I is gelijk
aan 1.
d(I1,
I2, ..., Ir, ..., In)
= 1 met Ir = (0, 0, ..., 1,
...,0) waarin de 1 op de re positie
staat en de rest van de elementen gelijk aan 0 is.
Door gebruik te maken van het Kronecker-symbool  ij
, gedefinieerd door ij
, gedefinieerd door
kunnen we ook Ir
= ( rj)
schrijven. rj)
schrijven.
|
|
Eigenschap IV is
niet zozeer een rij-eigenschap, maar meer een algemene eigenschap
die rechtstreeks uit de definitie voortvloeit.
Hier volgen de
bewijzen van de elementaire rij-eigenschappen:
Rij-eigenschap
I
Worden de elementen van een rij van een vierkant n ◊ n
matrix A = (aij)
met een constante  vermenigvuldigt, dan gaat det A over in
vermenigvuldigt, dan gaat det A over in  ∑ det A. Er geldt dus:
∑ det A. Er geldt dus:
d(A1,
A2, ... , ∑ Ar, ... , An)
=
∑ Ar, ... , An)
=  ∑
d(A1, A2, ... , Ar,
... , An) ∑
d(A1, A2, ... , Ar,
... , An)
Bewijs
Stel A' is de matrix die men krijgt door de elementen in de
r-e rij van matrix A met een constante  te vermenigvuldigen
te vermenigvuldigen
| A'
= |
 |
a11 |
a12 |
. |
. |
. |
a1n |
 |
| a21 |
a22 |
. |
. |
. |
a2n |
| . |
. |
|
|
|
. |
 ar1 ar1 |
 ar2 ar2 |
|
|
|
 arn arn |
| . |
. |
|
|
|
. |
| an1 |
an2 |
. |
. |
. |
ann |
Volgens de
definitie van de determinant geldt:
|
=  ∑
det A ∑
det A
|
Hetgeen te bewijzen viel.
Rij-eigenschap
II
Zij A' een n ◊ n matrix zodanig dat
| A'
= |
 |
a11 |
a12 |
. |
. |
. |
a1n |
 |
| a21 |
a22 |
. |
. |
. |
a2n |
| . |
. |
|
|
|
. |
| ar1+c1 |
ar2+c2 |
|
|
|
arn+cn |
| . |
. |
|
|
|
. |
| an1 |
an2 |
. |
. |
. |
ann |
dan geldt:
d(A1,
A2, ... , Ar + C, ... ,
An) = d(A1, A2,
... , Ar, ... , An) + d(A1,
A2, ... , C, ... , An)
Bewijs
Volgens de definitie van de determinant geldt:
Hetgeen te
bewijzen viel.
Rij-eigenschap
III
Verwisselt men in een vierkante n ◊ n matrix A = (aij)
de r-e met de l-e rij, dan wisselt det A
alleen van teken. Dus er geldt:
d(A1,
A2, ... , Ar, ... , Al,
... , An) = - d(A1,
A2, ... , Al, ... , Ar,
... , An)
Bewijs
Stel A is gegeven door
| A
= |
 |
a11 |
a12 |
. |
. |
. |
. |
a1n |
 |
|
| a21 |
a22 |
. |
. |
. |
. |
a2n |
|
| . |
. |
|
|
|
|
. |
|
| ar1 |
ar2 |
|
|
|
|
arn |
 r-e rij
r-e rij |
| . |
. |
|
|
|
|
. |
|
| al1 |
al2 |
|
|
|
|
aln |
 l-e rij
l-e rij |
| . |
. |
|
|
|
|
. |
|
| an1 |
an2 |
. |
. |
. |
. |
ann |
|
Stel V = { i
| i = 1,2, ..., n!} is de verzameling van
alle n! - zowel even als oneven - permutaties i
| i = 1,2, ..., n!} is de verzameling van
alle n! - zowel even als oneven - permutaties  i
van de natuurlijke getallen 1, 2, ... , n
met n i
van de natuurlijke getallen 1, 2, ... , n
met n  2.
2.
Door de permutatie  i
gaat de rangschikking i
gaat de rangschikking 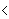 1,
2, ..., r, ... , l, ... , n 1,
2, ..., r, ... , l, ... , n dus over in de rangschikking
dus over in de rangschikking 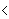  i(1), i(1),
 i(2),
... , i(2),
... ,  i(r),
... , i(r),
... ,  i(l),
... , i(l),
... ,  i(n) i(n) .Volgens
de definitie is .Volgens
de definitie is
Stel A' is
de matrix die men krijgt door in matrix A de r-e rij
met de l-e rij te verwisselen.
| A'
= |
 |
a11 |
a12 |
. |
. |
. |
. |
a1n |
 |
|
| a21 |
a22 |
. |
. |
. |
. |
a2n |
|
| . |
. |
|
|
|
|
. |
|
| al1 |
al2 |
|
|
|
|
aln |
 r-e rij
r-e rij |
| . |
. |
|
|
|
|
. |
|
| ar1 |
ar2 |
|
|
|
|
arn |
 l-e rij
l-e rij |
| . |
. |
|
|
|
|
. |
|
| an1 |
an2 |
. |
. |
. |
. |
ann |
|
Volgens de
definitie van de determinant geldt dan:
De permutatie  i
is gegeven door i
is gegeven door
 i
= i
= |
 |
1 |
2 |
... |
r |
... |
l |
... |
n |
 |
voor i = 1,2,
..., n! |
 i(1) i(1) |
 i(2) i(2) |
... |
 i(r) i(r) |
... |
 i(l) i(l) |
... |
 i(n) i(n) |
Zij nu  i'
gedefinieerd door i'
gedefinieerd door
 i'
= i'
= |
 |
 i'(
j) = i'(
j) =  i(
j) i(
j) |
voor j = 1, ..., n
en j 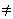 r, l
r, l |
voor i = 1,2, ..., n! |
 i'(
r) = i'(
r) =  i(
l) en i(
l) en  i'(
l) = i'(
l) =  i(
r) i(
r) |
De rangschikking 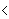  i'(1), i'(1),
 i'(2),
... , i'(2),
... ,  i'(r),
... , i'(r),
... ,  i'(l),
... , i'(l),
... ,  i'(n) i'(n) komt dus tot stand door in de rangschikking
komt dus tot stand door in de rangschikking 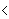  i(1), i(1),
 i(2),
... , i(2),
... ,  i(r),
... , i(r),
... ,  i(l),
... , i(l),
... ,  i(n) i(n) de elementen
de elementen  i(r)
en i(r)
en  i(l)
te verwisselen. Dus i(l)
te verwisselen. Dus
 i'
= i'
= |
 |
1 |
2 |
... |
r |
... |
l |
... |
n |
 |
voor i = 1,2,
..., n! |
 i(1) i(1) |
 i(2) i(2) |
... |
 i(l) i(l) |
... |
 i(r) i(r) |
... |
 i(n) i(n) |
Bij de
behandeling van permutaties en rangschikkingen hebben we gezien
dat dan geldt:
sgn( i)
= - sgn( i)
= - sgn( i') i')
Verder geldt dat V
= { i |
i = 1,2, ..., n!} = { i |
i = 1,2, ..., n!} = { i'
| i = 1,2, ..., n!}. i'
| i = 1,2, ..., n!}.
Alleen de volgorde in { i'
| i = 1,2, ..., n!} is anders dan in { i'
| i = 1,2, ..., n!} is anders dan in { i
| i = 1,2, ..., n!}. i
| i = 1,2, ..., n!}.
We kunnen
uitdrukking (2) nu schrijven als
Hetgeen te bewijzen viel.
Eigenschap
IV
De determinant van de n ◊ n
eenheidsmatrix I = (uij)is
gelijk aan 1.
Bewijs
Stel I is gegeven door
| I
= |
 |
1 |
0 |
0 |
. |
. |
. |
0 |
 |
| 0 |
1 |
0 |
. |
. |
. |
0 |
| 0 |
0 |
1 |
|
|
|
. |
| . |
. |
|
|
|
|
. |
| . |
. |
|
|
|
|
. |
| . |
. |
|
|
|
1 |
0 |
| 0 |
0 |
. |
. |
. |
0 |
1 |
Volgens de
definitie is
Voor de identieke
permutatie e geldt:
| sgn(e) ∑ u[1, 1] ∑
u[2, 2] . . . u[n, n] |
= |
1 ∑ 1 ∑ 1 . . . 1∑ |
|
= |
1 |
Voor alle andere
permutaties  i
in de uitdrukking (3) geldt: i
in de uitdrukking (3) geldt:
sgn( i)
∑ u[1, i)
∑ u[1,  i(1)]
∑ u[2, i(1)]
∑ u[2,  i(2)]
. . . u[n, i(2)]
. . . u[n,  i(n)]
= 0 i(n)]
= 0
omdat
er minstens ťťn factor u[r,  i(r)]
in voorkomt waarvoor r i(r)]
in voorkomt waarvoor r 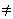
 i(r)
en dus u[r, i(r)
en dus u[r,  i(r)]
= 0. i(r)]
= 0.
Dus geldt det 1 = 1.
Hetgeen
te bewijzen viel.
Stellingen
Stelling
1
De determinant van een matrix waarvan een rijvector gelijk is aan O
= (0, 0, ... , 0), is gelijk aan 0.
Bewijs
We weten (Rij-eigenschap I) dat als we de elementen van
een rij van een vierkante n ◊ n matrix A = (aij)
met een constante  vermenigvuldigt, dan det A overgaat in
vermenigvuldigt, dan det A overgaat in  ∑ det A. Er geldt dus
∑ det A. Er geldt dus
d(A1,
A2, ... , ∑ Ar, ... , An)
=
∑ Ar, ... , An)
=  ∑
d(A1, A2, ... , Ar,
... , An) ∑
d(A1, A2, ... , Ar,
... , An)
Neem
nu eenvoudigweg  = 0
dan krijgen we: = 0
dan krijgen we:
d(A1,
A2, ... , O, ... , An)
= d(A1, A2, ... ,0 ∑
Ar, ... , An) = 0 ∑
d(A1, A2, ... , Ar,
... , An) = 0
Stelling
2
De determinant van een matrix waarvan twee rijen gelijk zijn, is
gelijk aan 0.
Bewijs
Beschouw een matrix A waarvan de r-e en
de l-e rij gelijk zijn. Dan geldt:
d(A1,
A2, ... , Ar, ... , Al,
... , An) = d(A1, A2,
... , Al, ... , Ar, ... , An)
(1)
Volgens
Rij-eigenschap III geldt echter ook:
d(A1,
A2, ... , Ar, ... , Al,
... , An) = - d(A1,
A2, ... , Al, ... , Ar,
... , An) (2)
Uit (1) en (2)
volgt:
d(A1,
A2, ... , Ar, ... , Al,
... , An) = - d(A1,
A2, ... , Ar, ... , Al,
... , An)
en dus
d(A1,
A2, ... , Ar, ... , Al,
... , An) = 0
Stelling
3
Als je in een matrix bij een rij een veelvoud van een andere rij
optelt, verandert de waarde van de determinant niet.
Bewijs
Beschouw een matrix A waarvan bij de r-e
rij een  -voud van de
l-e rij is opgeteld. Dan geldt volgens de rij-eigenschappen
I en II en stelling 2: -voud van de
l-e rij is opgeteld. Dan geldt volgens de rij-eigenschappen
I en II en stelling 2:
d(A1, A2, ...
, Ar +  Al,
... , Al, ... , An) Al,
... , Al, ... , An) |
= |
d(A1, A2, ...
, Ar, ... , Al, ... , An) |
|
|
+ d(A1, A2,
... ,  ∑
Al, ... , Al,
... , An) ∑
Al, ... , Al,
... , An) |
|
= |
d(A1, A2, ...
, Ar, ... , Al, ... , An) |
|
|
+  ∑
d(A1, A2, ... ,
Al, ... , Al,
... , An) ∑
d(A1, A2, ... ,
Al, ... , Al,
... , An) |
|
= |
d(A1, A2, ...
, Al, ... , Ar, ... , An) |
|
|
+  ∑
0 ∑
0 |
|
= |
d(A1, A2, ...
, Ar, ... , Al, ... , An) |
|
= |
det A |
Stelling
4
De determinant van een matrix waarvan de rijen afhankelijk zijn,
is gelijk aan 0.
Bewijs
Beschouw de matrix A waarvan de rijvectoren
afhankelijk zijn. Er bestaan dus scalairen (getallen)
c1, ... , cn, niet alle nul,
zodanig dat
| n |
 |
| i
= 1 |
|
ci ∑ Ai |
= |
O |
Dit betekent dat
elke rijvector Ar met cr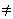 0
uitgedrukt kan worden als een lineaire combinatie van de andere
rijvectoren. Zonder de algemeenheid te schaden mogen we aannemen
dat A1 een lineaire combinatie van de andere
rijvectoren is: 0
uitgedrukt kan worden als een lineaire combinatie van de andere
rijvectoren. Zonder de algemeenheid te schaden mogen we aannemen
dat A1 een lineaire combinatie van de andere
rijvectoren is:
| A1 = |
| n |
 |
| i
= 2 |
|
ti ∑ Ai |
Daaruit volgt:
| d(A1, A2, ...
, An) |
= |
| d( |
| n |
 |
| i
= 2 |
|
ti ∑ Ai,
A2, ... , An) |
|
|
|
|
|
= |
| n |
 |
| i
= 2 |
|
ti ∑ d(Ai,
A2, ... , An) |
|
Elke term d(Ai,
A2, ... , An) in de laatste
som is gelijk aan 0 omdat Ai gelijk is aan
minstens ťťn van de andere rijvectoren A2, ...
, An. Dus de hele som is gelijk aan 0.
Hetgeen te
bewijzen viel.

Determinanten
berekenen
In het online computerprogramma "Matrixbewerkingen op
Internet" wordt van elke ingevoerde of berekende vierkante
matrix de waarde van de determinant direct op het scherm
afgedrukt.
De definitie van de determinant, zoals die hier gegeven is, is op
zich niet erg geschikt om gebruikt te worden voor het berekenen
van een determinant in een computerprogramma.
…ťn van de
beste methoden om m.b.v. een computerprogramma de determinant van
een matrix A uit te rekenen, is de Gauss-Jordan eliminatie
methode. Deze methode houdt in dat we matrix A
| A
= |
 |
a11 |
a12 |
. |
. |
. |
a1n |
 |
| a21 |
a22 |
. |
. |
. |
a2n |
| . |
. |
|
|
|
. |
| ar1 |
ar2 |
. |
. |
. |
arn |
| . |
. |
|
|
|
. |
| an1 |
an2 |
. |
. |
. |
ann |
d.m.v elementaire
rij-operaties tot een bovendiagonaalmatrix D
| D
= |
 |
d11 |
d12 |
. |
. |
. |
d1n |
 |
| 0 |
d22 |
. |
. |
. |
d2n |
| . |
. |
|
|
|
. |
| . |
. |
|
|
|
. |
| . |
. |
|
|
|
. |
| 0 |
0 |
. |
. |
. |
dnn |
kunnen herleiden
door:
-
twee rijen
verwisselen
-
een rij met
een scalair  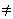 0 vermenigvuldigen;
0 vermenigvuldigen;
-
bij een rij
een  -voud
van een andere rij optellen. -voud
van een andere rij optellen.
Bij operatie 1.
wisselt de determinant van teken, bij operatie 2. wordt de waarde
van de determinant met  vermenigvuldigt en bij operatie 3. verandert de waarde van de
determinant niet.
vermenigvuldigt en bij operatie 3. verandert de waarde van de
determinant niet.
Door de operaties
1., 2. en 3. systematisch op de matrix A toe te passen,
kunnen we deze herleiden tot een bovendiagonaalmatrix D,
waarvan we de determinant eenvoudig kunnen bereken. Bij elke
operatie 1. of 2. moeten we uiteraard bijhouden hoe de determinant
verandert.
Stel we hebben
operatie 1. p keer en operatie 2. q keer
toe moeten passen om matrix A te herleiden tot een
bovendiagonaalmatrix D. Stel dat bij operatie 2. de
vermenigvuldigingsfactoren
 1, 1,  2, 2,
 3, ... 3, ...  q
gebruikt zijn. Dan krijgen we: q
gebruikt zijn. Dan krijgen we:
det A = (-1)
p ( 1 1
 2 2  3
... 3
...  q)-1
∑ det D, met det D
= d11 d22 d33
. . . dnn q)-1
∑ det D, met det D
= d11 d22 d33
. . . dnn
Ga dit na!

Voorbeeld
| det |
 |
1 |
3 |
 |
| 2 |
8 |
|
= 2; det |
 |
5 |
0 |
1 |
 |
| 1 |
-2 |
3 |
| 3 |
8 |
6 |
|
= -166 |
Ga dit voorbeeld
met onderstaand programma na.
Kies uit het Bestand-menu het item Nieuw Project.
Kies daarna het project C = A-1
(het inverteren van matrices) en vul de matrixelementen in.

Het
programma (programma-handleiding)
|

