|
Inleiding
De vergelijking 5x2
+ 2 = 2x + 7 is
een voorbeeld van een kwadratische vergelijking. In plaats
van kwadratische vergelijking spreken we ook wel van vierkantsvergelijking.
In een kwadratische vergelijking komen dus kwadratische termen
zoals in dit geval 5x2
voor. Er komen geen derdegraads termen zoals 2x3
of nog hogere machten van x in
voor.
Elke kwadratische
vergelijking kan altijd tot één van de drie onderstaande
typen herleid worden.
-
x2
= p
-
ax2
+ bx
= 0
-
ax2
+ bx
+ c = 0
Op deze webpagina
gaan we type 2 bestuderen.
In type 2 en 3 komen ook nog eerstegraads termen van x
voor en zijn beide op 0 herleid, d.w.z. zij eindigen beide op ....
= 0. Bij type 1 hoeft de waarde van p
niet gelijk aan 0 te zijn. Bij het het herleiden van kwadratische
vergelijkingen naar één van de bovenstaande standaardvormen moet
je in ieder geval een aantal basisregels in acht nemen.
-
Je mag bij
beide leden van de vergelijking hetzelfde getal optellen of
van beide leden hetzelfde getal aftrekken.
-
Je mag beide
leden van de vergelijking met hetzelfde getal
 0
vermenigvuldigen of door hetzelfde getal 0
vermenigvuldigen of door hetzelfde getal
 0
delen. 0
delen.
We noemen dit
ook wel het "weegschaalmodel" omdat de balans in
evenwicht blijft als je aan beide kanten van de weegschaal maar
dezelfde gewichten toevoegt of weghaalt.
Type 1 en 2
kunnen daarna volgens vaste regels opgelost worden. Bij type 3
hangt de oplossingsmethode een beetje af van de waarden van a,
b en c
en of je daarbij herkent welke oplossingsmethode het makkelijkst
is. De makkelijkste methode is "ontbinden in factoren",
maar deze kan lang niet altijd toegepast worden. Een methode die
wel altijd toegepast kan worden is het gebruik van de abc-formule.
Alle
soorten kwadratische vergelijkingen en hun oplossingsmethoden
worden op deze website behandeld en kun je via het
"Lessen online" menu bereiken.

Kwadratische
vergelijkingen van het type ax2
+ bx
= 0
Ook dit type is eenvoudig oplosbaar. Dus je hebt
weer geluk als je een kwadratische vergelijking tot deze vorm kunt
herleiden. Hieronder zie je het oplossingsschema.
| ax2
+ bx
= 0 |
 x(ax
+ b) = 0
x(ax
+ b) = 0 |
|
 x
= 0 of ax
+ b = 0
x
= 0 of ax
+ b = 0 |
|
 x
= 0 of ax
= -b
x
= 0 of ax
= -b |
|
 x
= 0 of x
= -
x
= 0 of x
= - |
We bestuderen
deze oplossingsmethode aan de hand van een aantal voorbeelden.

Voorbeeld
1
Een voorbeeld van
dit type is:
x2
+ 5x
= 0
We
gaan de oplossingsmethode stap voor stap bekijken:
-
De
termen x2
( = x·
x)
en 5x
( = 5·
x)
bevatten beide minimaal één factor x.
We kunnen dus één factor x
buiten haakjes halen. We krijgen dan:
x(x
+ 5)
= 0
We
zeggen ook wel dat we x2
+ 5x
ontbonden hebben in twee factoren
x en (x
+ 5).
-
We
hebben nu dus een product van twee factoren xen
(x
+ 5)
waarvan de waarde gelijk aan 0 is. Dit betekent dat er twee
mogelijkheden zijn:
x
= 0 òf x
+ 5 =
0 oftewel x = 0
òf x = -
5
-
De
oplossingen van x2
+ 5x
= 0 zijn dus x
= 0 en x
= - 5.
Er zijn dus twee oplossingen! Je kunt gemakkelijk nagaan dat
dit ook klopt door deze waarden van x in de
vergelijking in te vullen. Je ziet dan dat er inderdaad 0 uit
komt. Ga dit na!

Voorbeeld
2
Een tweede voorbeeld van dit type is:
3x2
- 2x
= 0
We gaan ook hier
weer de oplossingsmethode stap voor stap bekijken:
-
Vermenigvuldig
eerst beide leden van de vergelijking met
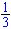 ( het omgekeerde
( het omgekeerde
van 3).
Je krijgt dan:
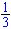 (3x2
- 2x)
= (3x2
- 2x)
=
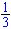 · 0 = 0
· 0 = 0
-
Werk
nu nog de haakjes weg. Dan krijg je:
1x2
-
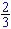 x
= 0 oftewel x2
- x
= 0 oftewel x2
-
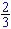 x
= 0 x
= 0
We
hebben natuurlijk met opzet beide leden van de vergelijking met
het omgekeerde van 3
vermenigvuldigd want:
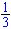 · 3 = 1
en verder is
· 3 = 1
en verder is
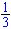 · 2 =
· 2 =
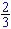 . .
-
De
termen x2
(= x·
x) en
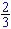 x
(= x
(=
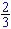 · x) bevatten
beide minimaal één factor x.
We kunnen dus één factor x
buiten haakjes halen. We krijgen dan:
· x) bevatten
beide minimaal één factor x.
We kunnen dus één factor x
buiten haakjes halen. We krijgen dan:
x(x
-
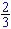 )
= 0 )
= 0
We
zeggen ook wel dat we x2
-
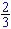 x
ontbonden hebben in twee factoren x
ontbonden hebben in twee factoren
x en (x
-
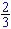 ). ).
-
We
hebben nu dus een product van twee factoren x
en (x
-
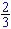 )
waarvan de waarde gelijk aan 0 is. Dit betekent dat er twee
mogelijkheden zijn: )
waarvan de waarde gelijk aan 0 is. Dit betekent dat er twee
mogelijkheden zijn:
x
= 0 òf ( x
-
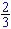 )
= 0 oftewel x =
0 òf x = )
= 0 oftewel x =
0 òf x =
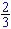
-
De
oplossingen van 3x2
- 2x
= 0 zijn dus x
= 0 en x =
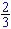 .
Er zijn dus twee oplossingen! Je kunt gemakkelijk nagaan dat
dit ook klopt door deze waarden van x in de
vergelijking in te vullen. Je ziet dan dat er inderdaad 0 uit
komt. Ga dit na! .
Er zijn dus twee oplossingen! Je kunt gemakkelijk nagaan dat
dit ook klopt door deze waarden van x in de
vergelijking in te vullen. Je ziet dan dat er inderdaad 0 uit
komt. Ga dit na!

Voorbeeld
3
Een derde voorbeeld met breuken van dit type is:
2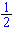 x2
- 3 x2
- 3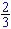 x
= 0 x
= 0
We gaan ook hier
weer de oplossingsmethode stap voor stap bekijken:
-
Vermenigvuldig
eerst beide leden van de vergelijking met
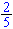 ( het omgekeerde
( het omgekeerde
van 2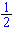 =
=
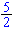 ).
Je krijgt dan: ).
Je krijgt dan:
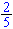 (2
(2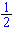 x2
- 3 x2
- 3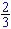 x)
= x)
=
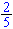 ·
0 = 0 ·
0 = 0
-
Werk
nu nog de haakjes weg. Dan krijg je:
1x2
-
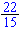 x
= 0 oftewel x2
- 1 x
= 0 oftewel x2
- 1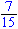 x
= 0 x
= 0
We
hebben natuurlijk met opzet beide leden van de vergelijking met
het omgekeerde van 2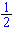 vermenigvuldigd want:
vermenigvuldigd want:
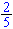 · 2
· 2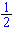 =
=
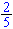 · ·
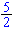 = 1 en verder is
= 1 en verder is
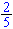 · 3
· 3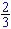 =
=
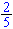 · ·
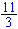 =
=
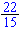 = 1
= 1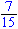
-
De
termen x2
(= x·
x) en 1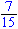 x
(= 1 x
(= 1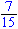 ·
x)
bevatten beide minimaal één factor x.
We kunnen dus één factor x
buiten haakjes halen. We krijgen dan: ·
x)
bevatten beide minimaal één factor x.
We kunnen dus één factor x
buiten haakjes halen. We krijgen dan:
x(x
- 1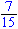 )
= 0 )
= 0
We
zeggen ook wel dat we x2
- 1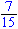 x
ontbonden hebben in twee factoren x
en (x
- 1 x
ontbonden hebben in twee factoren x
en (x
- 1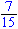 ). ).
-
We
hebben nu dus een product van twee factoren x
en (x
- 1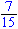 )
waarvan de waarde gelijk aan 0 is. Dit betekent dat er twee
mogelijkheden zijn: )
waarvan de waarde gelijk aan 0 is. Dit betekent dat er twee
mogelijkheden zijn:
x
= 0 òf (x
- 1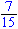 )
= 0 oftewel x
= 0 òf x = 1 )
= 0 oftewel x
= 0 òf x = 1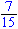
-
De
oplossingen van 2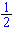 x2
- 3 x2
- 3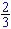 x
= 0 zijn dus x
= 0 en x =
1 x
= 0 zijn dus x
= 0 en x =
1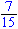 .
Er zijn dus twee oplossingen! Je kunt gemakkelijk nagaan dat
dit ook klopt door deze waarden van x in de
vergelijking in te vullen. Je ziet dan dat er inderdaad 0 uit
komt. Ga dit na! .
Er zijn dus twee oplossingen! Je kunt gemakkelijk nagaan dat
dit ook klopt door deze waarden van x in de
vergelijking in te vullen. Je ziet dan dat er inderdaad 0 uit
komt. Ga dit na!

Opgaven
- Los op
-
4x2
-
5 = 6x -
5
-
9x
+ 7 = 7(x2 + 1)
-
4x2
-
4 = 4(2x -
1)
-
8(x
-
1) = 4(2 -
x2) -
16
-
3(x
-
2) = 5(x2 -
3) + 9
-
5x
-
3 = 3(x2 -
1)
-
Los op
-
2(3x
+ 7) = x -
(2x2 -
14)
-
2.8x2
-
1.5 = 5.3x -
1.5
-
0.3x2
+ 7.5 = 5 -
2.5(x -
1)
-
3x
-
8 = 2x2 -
(x + 8)
Maak eerst zelf de
opgaven alvorens je de uitwerkingen gaat bekijken.
Uitwerkingen

|

